《二哥的 LeetCode 刷题笔记》真的容易懂。 ------------------------by鲁迅

题意

给你一个字符串 s，找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

难度

中等

分析 1

要解这道题，我们需要搞清楚几个概念：

• 什么是字符串的反序？
• 什么是回文串？
• 什么是最长回文子串？

首先，字符串的反序就是将字符串中的字符顺序颠倒过来，例如：abc的反序就是cba。

其次，回文串就是正着看和反着看是一样的字符串，例如：abcba就是一个回文串，因为反着看也是abcba。

最后，最长回文子串就是在一个字符串中，最长的回文串，例如：abcba的最长回文子串就是abcba，而示例中的babad的最长回文子串就是bab或者aba。

那搞清楚这几个概念后，我们就很容易想到暴力解法：截取每一段子串，然后判断它是不是回文串，如果是的话，就更新最长回文子串。

class Solution {
    // 辅助函数，用于检查字符串 s 中从索引 begin 到 end 的子串是否为回文
    boolean isPalindrome(String s, int begin, int end) {
        while (begin <= end) {
            // 如果两端的字符不同，则不是回文
            if (s.charAt(begin) != s.charAt(end))
                return false;
            // 向中间移动
            begin++;
            end--;
        }
        // 如果所有字符都相同，则是回文
        return true;
    }

    // 主函数，用于找出字符串 s 中的最长回文子串
    public String longestPalindrome(String s) {
        int ansl = 0, ansr = 0; // 存储最长回文子串的起始和结束索引
        // 外层循环遍历子串的起始位置
        for (int i = 0; i < s.length(); i++)
            // 内层循环遍历子串的结束位置
            for (int j = i; j < s.length(); j++)
                // 检查子串是否是回文
                if (isPalindrome(s, i, j)) {
                    // 如果找到更长的回文子串，则更新最长回文子串的索引
                    if (j - i > ansr - ansl) {
                        ansr = j;
                        ansl = i;
                    }
                }
        // 返回最长回文子串
        return s.substring(ansl, ansr + 1);
    }
}

但是，结果非常感人……

完全无法接受的结果，两层循环 $O(n^2)$ 的时间复杂度，再加上判断回文串又是 $O(n)$ 的时间复杂度，所以总共是 $O(n^3)$ 的时间复杂度，这完完全全超出了题目预期的范围。

分析 2

我们来想想其他的方法。

“回文串”，意思就是正着看和反着看是一样的。

那我们是不是能够通过求这个字符串倒置之后的串和原串的最长公共子串，得到的这个最长公共子串，也就是原串的最长回文子串？

是的，见下图。

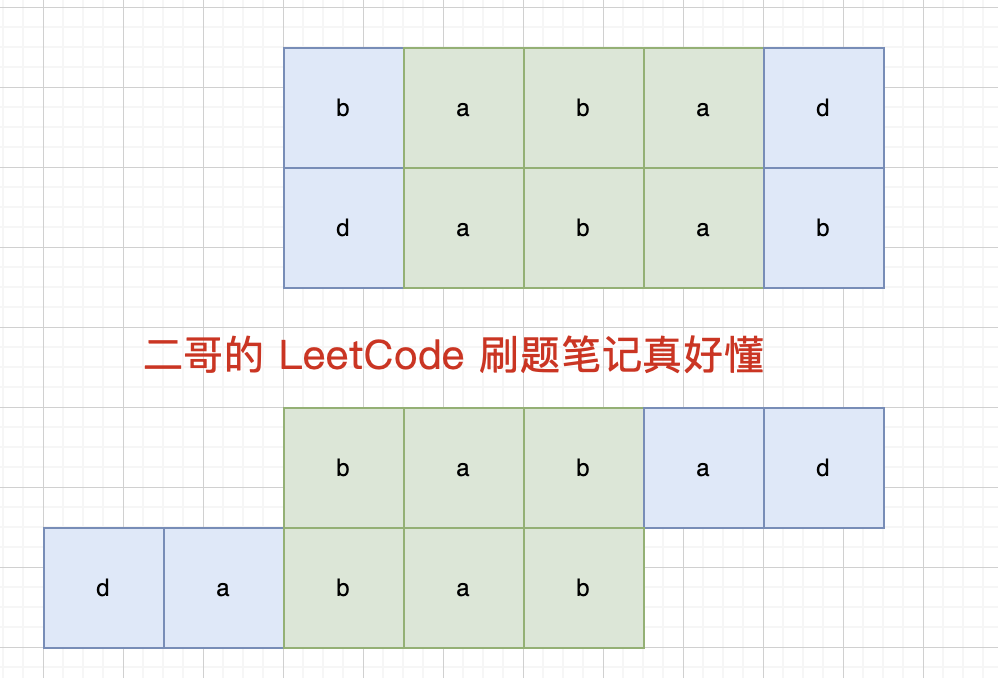
但是有一个问题。

例如：adccdcda，它倒置之后是adcdccda，两个串的最长公共子串则是adc或者cda，可是这两个显然不是回文子串。

问题就出在位置的判断上。

除了要判断是不是最长公共子串，还需要多一个判断，看看这个最长公共子串在原串中的位置和倒置之后的串中的位置是不是对应的。

求解两个字符串的最长公共子串，我们可以用动态规划来解决。

什么是动态规划？

动态规划（Dynamic programming，简称 DP）是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于暴力解法。

简单来说，动态规划其实就是，给定一个问题，我们把它分解成若干个子问题，直到子问题可以直接求解，然后再逐步合并子问题的解，最终得到原问题的解。

动态规划的核心思想就是记住已经解决过的子问题的解，避免重复计算。

来看一个比较经典的例子：

• Q：1+1+1+1+1=？
• A：5
• Q：在等号左边再+1 呢？
• A：6
• Q：你怎么这么快就知道答案了？
• A：我记住了，1+1+1+1+1=5，再+1就是6了。

这就是动态规划的核心思想，记住已经解决过的子问题的解，避免重复计算。

再来看一个更经典的例子：斐波那契数列。

斐波那契数列是这样一个数列：1、1、2、3、5、8、13、21、34、……，即第一项和第二项为1，第三项为前两项之和，第四项为前两项之和，以此类推。

我们可以用递归的方式来求解斐波那契数列，但是递归的方式会有很多重复计算，例如：求解第5项的时候，需要先求解第4项和第3项，求解第4项的时候，需要先求解第3项和第2项，求解第3项的时候，需要先求解第2项和第1项；求解第4项的时候，需要先求解第3项和第2项，求解第3项的时候，需要先求解第2项和第1项；求解第3项的时候，需要先求解第2项和第1项；求解第2项的时候，需要先求解第1项；求解第1项的时候，直接返回1。

用代码表示就是这样的：

class Solution {
	// 递归求解斐波那契数列
	public int fib(int n) {
		if (n == 1 || n == 2)
			return 1;
		return fib(n - 1) + fib(n - 2);
	}
}

那如果用动态规划的方式来求解斐波那契数列呢？

我们可以用一个数组来存储已经求解过的子问题的解，这样就可以避免重复计算了。

class Solution {
	// 动态规划求解斐波那契数列
	public int fib(int n) {
		int[] f = new int[n + 1];
		f[1] = f[2] = 1;
		for (int i = 3; i <= n; i++)
			f[i] = f[i - 1] + f[i - 2];
		return f[n];
	}
}

大家可以感受一下递归和动态规划两种方式求解斐波那契数列的不同。

递归是，以前哪怕计算过，比如说求第 4 项的时候已经计算过第 3 项了，但是求第 5 项的时候还是要重新计算第 3 项，这就是重复计算。

但动态规划是，以前计算过的结果我都保留下来，下次用到的时候直接拿来用，不用重新计算。比如说求第 4 项的时候已经计算过第 3 项了，求第 5 项的时候直接拿第 4 项和第 3 项的结果相加就可以了。

OK，相信大家都明白了动态规划的内核了。

如果还需要补充资料，可以看看这个帖子，里面还会讲到贪心和动态规划的区别，讲的很好：https://www.zhihu.com/question/23995189/answer/613096905

那我们来继续解这道题。

第一步，反转原始字符串 s，得到字符串 rev。

第二步，使用一个二维数组 f[][] 来记录 s 和 rev 之间的最长公共子串的长度。f[i][j] 表示 s 中以 i 结尾和 rev 中以 j 结尾的子串的最长公共后缀的长度。

对二维数组比较陌生的球友可以先看一下《二哥的 Java 进阶之路》中这篇内容：掌握 Java二维数组

第三步，填充动态规划表，遍历这两个字符串，对于每一对字符 s[i] 和 rev[j]：

• 如果 s[i] == rev[j]，则 f[i][j] = f[i-1][j-1] + 1。这表示当前字符匹配，并且可以在之前的最长公共后缀上增加一个字符。
• 否则，f[i][j] 保持为 0。

第四步，检查回文条件，在填充表的过程中，每次 f[i][j] 被更新时，我们需要检查是否满足回文条件。

即检查以 i 结尾的 s 的子串是否真的是一个回文串，通过检查 f[i][j] 对应的子串的起始位置是否正确。如果 f[i][j] 是回文，并且是到目前为止找到的最长的，我们更新最长回文子串的长度和起始位置。

最后，根据记录的最长长度和起始位置，从原始字符串 s 中提取出最长的回文子串。

class Solution {
    public String longestPalindrome(String s) {
        // 反转原始字符串
        String rev = new StringBuffer(s).reverse().toString();
        int n = s.length();

        // 动态规划数组，f[i]...